Tcl – 再帰呼び出し

再帰呼び出し(recursive call)

procコマンドで定義した手続きの中で、その手続きと同じプロシージャ(自分自身)を再び呼び出す事を再帰呼び出しと言います。

再帰呼び出しは階乗、累乗など再帰的な構造をもつアルゴリズムで使われることがあります。

再帰呼び出しを記述するには、以下のようにします。

• 定義した手続きの中で自分自身を呼び出す。
• 必ず終了条件を記述する。

再帰呼び出しの利点と欠点

利点

• ループ処理を簡潔に記述できるので手続きの構造がすっきりする。

欠点

• 呼び出しを行うごとに、手続きをメモリへ展開する為、効率が悪く、処理速度はあまり期待できない。
• 終了条件を誤ると無限ループやスタックオーバフローを引き起こす危険性があるので注意が必要。

再帰的な構造の作り方

再帰の説明で良くある例は、階乗を求めるプログラムですが、「階乗って何？」という方もいるかも知れないので、まずは、hello!を５回出力するプログラムを再帰呼び出しを使用しない場合と使用した場合の例で説明します。

[再帰呼び出しを使用しない例] サンプル：print_str.tcl

#!/bin/sh
# the next line restarts using tclsh \
exec tclsh "$0" "$@"

# 文字列を指定した回数出力する(ループ)

proc Print {str n} {
    while {$n > 0} {
        puts $str
        incr n -1
    }
    return 0
}

# main

Print hello! 5

[実行例]

$ ./print_str.tcl
hello!
hello!
hello!
hello!
hello!

上のサンプルを再帰呼び出しを使用すると以下のようになります。

[再帰呼び出しを使用した例] サンプル：print_str2.tcl

#!/bin/sh
# the next line restarts using tclsh \
exec tclsh "$0" "$@"

# 文字列を指定した回数出力する(再帰呼び出し)

proc Print {str n} {
    if {$n == 0} {
        return 0
    } else {
        puts $str
        Print $str [expr $n - 1]  ;# 再帰呼出
    }
}

# main

Print hello! 5

[実行例]

$ ./print_str2.tcl
hello!
hello!
hello!
hello!
hello!

Print $str [expr $n -1] を実行する度に、変数nは、以下のように変化していきます。

5 → 4 → 3 → 2 → 1 → 0

＜再帰呼び出しのイメージ＞

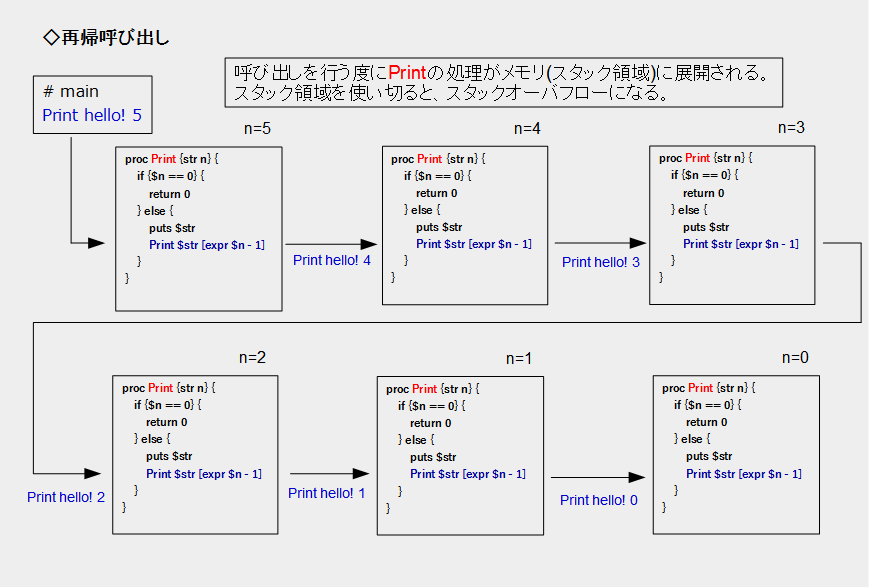
最初に、再帰呼び出しは自分自身を呼び出すと説明しましたが、上の図を見てわかるように実際には、

　Print $str [expr $n -1]

を実行すると、自分と同じ処理をする別の手続き(クローン)を呼び出しています。

呼び出しをするたびに変数nは減少していき、最終的にn=0になり、処理を終了します。

再帰を利用したプログラム

再帰呼び出しを利用したプログラムを２つ紹介します。

階乗(factorial)

階乗とは1からある数字まで連続する整数の積のことです。1からnまで連続する整数の積をnの階乗といい、「n!」と表記します。

階乗の定義

　n! = n x (n – 1)!
　0! = 1

例. 5! は、 5 x 4 x 3 x 2 x 1 で、120になります。

階乗を使うと何通りの組み合わせがあるか計算できます。5枚のカードの組み合わせは120通りです。

ちなみに、0!=1 と定義されています。理由を知りたい方はネットで検索してください。

[サンプル] fact.tcl

#!/bin/sh
# the next line restarts using tclsh \
exec tclsh "$0" "$@"

# 階乗計算
proc fact {n} {
    if {$n > 0} {
        return [expr $n * [fact [expr $n - 1]]]
    } else {
        return 1  ;# 0!=1
    }
}

## main ##

set n 5  ;# 数値

# 結果
puts "$n! = [fact $n]"

[実行例]

$ ./fact.tcl
5! = 120

fact 5 は 5!を計算します。

プロシージャのfact {n} を fact [expr n-1] で再帰呼び出ししています。

階乗の定義は、n! = n x (n -1)!、 0! = 1 なので以下の関係になります。

　5! = 5 x 4! → 5 x fact 4 → 120
　4! = 4 x 3! → 4 x fact 3 → 24
　3! = 3 x 2! → 3 x fact 2 → 6
　2! = 2 x 1! → 2 x fact 1 → 2
　1! = 1 x 0! → 1 x fact 0 → 1
　0! = 1

累乗(repeated multiplication)

累乗とは同じ数字を繰り返し掛算したものです。aをn回かけ算したものをaのn乗といい「aⁿ」と表記します。また、aのことを低、nのことを指数といいます。

指数を上付き文字で表現できない場合は「a^n」のように書きます。

例.5の3乗は5 x 5 x 5 で、125になります。

階乗の時と同じように以下の関係になります。

　　5³ = 5×5²
　　5² = 5×5¹
　　5¹ = 5×5⁰

累乗の定義は以下になります。

　　aⁿ = a x aⁿ⁻¹
　　a⁰ = 1

累乗を計算するプログラムを再帰呼び出しを使って記述すると以下のようになります。

[サンプル] pow.tcl

#!/bin/sh
# the next line restarts using tclsh \
exec tclsh "$0" "$@"

# 累乗計算
proc pow {a n} {
    if {$n > 0} {
        return [expr $a * [pow $a [expr $n - 1]]]
    } else {
        return 1  ;# a^0=1
    }
}

## main ##

set a 5  ;# 低
set n 3  ;# 指数

# 結果
puts "$a^$n = [pow $a $n]"

[実行例]

$ ./pow.tcl
5^3 = 125

累乗の計算を使うことで、2進数のn桁目の値や最大値を計算できます。

a=2 n=3 に変えて計算すると、2^3 = 8 になります。
a=2 n=4 に変えて計算すると、2^4 = 16 になります。

4ビットは0～3bitの4桁なので、3bit目は8になります。表現できる範囲は10進数で0～15の16個(0を含む)になります。

　2⁴ = 16
　2³ = 8
　2² = 4
　2¹ = 2
　2⁰ = 1

[参考]

　1K → 2^10 = 1,024
　4K → 2^12 = 4,096
　1M → 2^20 = 1,048,576
　1G → 2^30 = 1,073,741,824
　4G → 2^32 = 4,294,967,296
　※32bit CPU、4GBの壁