この記事は配列のハッシュテーブルの統計情報を表示するオプション(statistics)の使い方とハッシュテーブルについて紹介します。
ハッシュテーブルの統計情報
[書式]
array statistics arrayName配列を表すハッシュテーブル内のデータの分布に関する統計を返します。この情報には、テーブル内のエントリ数、バケット数、およびバケットの使用率が含まれます。
[使用例]
% array set progress {
00:00 開始
00:10 進捗1
00:30 進捗2
01:00 進捗3
02:00 終了
}
% array statistics progress
5 entries in table, 4 buckets ----(1)
number of buckets with 0 entries: 0 ----(2)
number of buckets with 1 entries: 3
number of buckets with 2 entries: 1
number of buckets with 3 entries: 0
number of buckets with 4 entries: 0
number of buckets with 5 entries: 0
number of buckets with 6 entries: 0
number of buckets with 7 entries: 0
number of buckets with 8 entries: 0
number of buckets with 9 entries: 0
number of buckets with 10 or more entries: 0 ----(3)
average search distance for entry: 1.2 ----(4)出力メッセージは以下のような意味になります。
x entries in table, y buckets
ハッシュテーブル内の分布。
エントリ数:x個 バケット数:y個
number of buckets with x entries: y
x個のエントリを持つバケット数:y個
number of buckets with 10 or more entries: y
10個以上のエントリ数を持つバケット数:y個
※同じハッシュ値の要素を10個以上連結したリストを持つバケットの数。
average search distance for entry: z
エントリの平均探索距離:z
※この数値が大きいと探索に時間がかかる要素数の比率が高い。
統計情報の出力メッセージの内容は、ハッシュテーブルがどのようなものか分かっていないと、意味が理解できないと思います。
ハッシュテーブルを説明したWikipediaのページを紹介しておきます。
https://ja.wikipedia.org/wiki/ハッシュテーブル
https://ja.wikipedia.org/wiki/ハッシュ関数
ハッシュテーブル
ハッシュテーブルがどのようなものか、Wikipediaのページを見ても理解出来ないかもしれないので、ハッシュテーブルのイメージ図と簡単な説明を以下に記載しました。
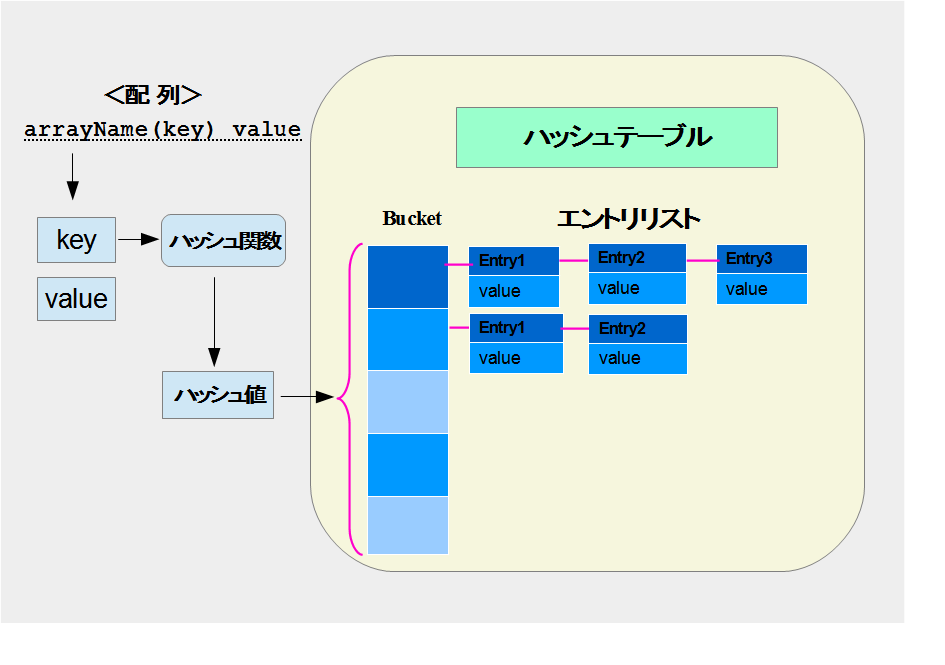
◇ハッシュに関連する用語の説明
ハッシュ(hash)とは
英語でhashとは、細かく刻む、寄せ集め、ごたまぜ、などの意味。
ハッシュ関数
キー(key)からハッシュ値を得る関数。ハッシュ関数は、入力された、キー(key)をもとに、何らかの規則に従ってハッシュ値を生成します。
例えば、キーで使用される文字コードを全て加算して100で割った余りをハッシュ値として使用するなど。
ハッシュ値
連想配列のハッシュテーブルで使用するハッシュ値は、キー(key)をもとに、ハッシュ関数で生成した値のこと。ハッシュ値のことをバケットインデックスともいう。
バケット(bucket)
ハッシュテーブルの各要素。スロットともいう。
エントリ
1つまたは同じハッシュ値をもつ複数の要素。
ハッシュテーブル(hash table)
ハッシュテーブルは、ハッシュ値をインデックスとした値の組(エントリ)を格納できるデータ構造持った配列です。ハッシュテーブルのことをハッシュ表ともいう。
ハッシュ法とは
キーからハッシュ関数によりハッシュ値を生成し、データが格納されている位置(バケット)に直接結び付けることにより、高速に探索する。この方法をハッシュ法という。
◇ハッシュ関数の問題点
ハッシュ関数は、同じキーが入力されると同じハッシュ値を生成します。キーが異なると全く別のハッシュ値が生成されることが望ましいが、ハッシュ関数の作りによっては、同じハッシュ値を生成する事がある。これを衝突(collision)という。
◇衝突に対する対策
チェイン法(chaining)
同じハッシュ値を持つデータを連結リストで繋いでおく。バケットには連結リストのリンク(リンクリスト)が格納される。
探索方法は
- ハッシュ値から探索するバケットに関連付ける。
- バケットのリストを探索する。
欠点:リストが長くなると探索が遅くなる。
オープンアドレス法(open addressing)
衝突が発生した時に、ある手順に従って別のバケット(空のバケット)を探して、データを格納する。これを再ハッシュという。オープンアドレス法は開番地法とも呼ばれています。
バケットにはデータそのものが格納される。
欠点:ハッシュテーブルのバケットが一杯になれば、それ以上のデータを登録できない。
◇ハッシュ、ハッシュ値の特長と利用場面
ハッシュ、ハッシュ値の特長
- 同じ入力データからは同じハッシュ値が生成されます。
- 入力データが少しでも異なれば違うハッシュ値が生成されます。
※ただしハッシュ関数の作りによっては同じハッシュ値を生成する事があります。 - 生成されたハッシュ値は不可逆的であり、ハッシュ値から元のデータを復元・推測することは困難。
このような特長があることから、ハッシュは、ファイルや入力データの改ざん防止、パスワードの認証、デジタル署名、ブロックチェーンの改ざん防止などにも使用されています。
代表的なハッシュ関数としては、SHA,MD5があります。
統計情報の出力サンプル
配列をn個作成して、作成した配列のハッシュテーブルの分布がどのようになっているか、統計情報を出力してメッセージを確認してみました。
サンプルコード: mkarr.tcl 指定した個数の配列を作る。
# 配列をn個作る
set n 1000
for {set key 0} {$key < $n} {incr key} {
set arr($key) [expr int (rand() * $n)]
}[expr int (rand() * $n)] で0からn未満の乱数を生成します。
上のサンプルコードのファイルを利用して配列を作成します。
[やり方]
- 作成する配列の個数は変数nの値を変更します。
- sourceコマンドでmkarr.tclを読み込む。
- array statisticsコマンドで統計情報を出力する。
統計情報の出力抜粋(要素数1~5個)
# 要素数1個の場合
1 entries in table, 4 buckets
number of buckets with 0 entries: 3
number of buckets with 1 entries: 1
・
・
average search distance for entry: 1.0
# 要素数4個の場合
4 entries in table, 4 buckets
number of buckets with 0 entries: 0
number of buckets with 1 entries: 4
・
・
average search distance for entry: 1.0
# 要素数5個の場合
% array statistics arr
5 entries in table, 4 buckets
number of buckets with 0 entries: 0
number of buckets with 1 entries: 3
number of buckets with 2 entries: 1
・
・
average search distance for entry: 1.2
<上記出力の説明>
〇 1 entries in table, 4 buckets より
要素数が1つでも4バケット分作られるようです。
〇 number of buckets with 0 entries: 3 の意味
空(未使用)のバケットが3個あるという意味です。
〇average search distance for entry: 1.2
英語を日本語に直訳すと、「エントリの平均探索距離」という意味ですが、「平均探索距離?」て日本語の感覚で考えるとイマイチわからないですよね。
エントリを探し出すまでの距離(間隔)の平均値ということなので、「ある値の探索にかかる実行回数の平均値」と訳した方がすっきりするかも。
要素数4個までは、この値が「1.0」です。これは、使用済みの各バケットにはエントリが1つしかないので当然です。
要素数5個の場合は、この値が「1.2」です。この値は以下の式で計算できます
(各エントリの探索回数の総数)/(エントリ数)
<要素数5個の場合のハッシュテーブルイメージ>

探索に必要な手順の回数は、A1~D1の1列目は1手順、D2の2列目は2手順かかるので総回数は6回になります。
よって、6÷5=1.2 になります。
数を増やして要素数10個で考えた方が理解しやすいかも知れませんね。
統計情報の出力抜粋(要素数10個)
% array statistics arr
10 entries in table, 4 buckets
number of buckets with 0 entries: 0
number of buckets with 1 entries: 0
number of buckets with 2 entries: 2
number of buckets with 3 entries: 2
number of buckets with 4 entries: 0
number of buckets with 5 entries: 0
number of buckets with 6 entries: 0
number of buckets with 7 entries: 0
number of buckets with 8 entries: 0
number of buckets with 9 entries: 0
number of buckets with 10 or more entries: 0
average search distance for entry: 1.8<要素数10個の場合のハッシュテーブルイメージ>
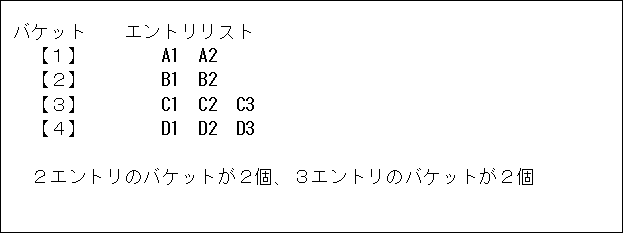
1列目 A1~D1 は1回(距離が1つ離れている) 1×4=4
2列目 A2~D2 は2回(距離が2つ離れている) 2×4=8
3列目 C3~D3 は3回(距離が3つ離れている) 3×2=6
合計:18
(各エントリの探索回数の総数)/(エントリ数)なので
18÷10=1.8
あってますよね。
以下は、要素数が、10万個、100万個の場合のサンプルです。
統計情報の出力抜粋(10万個、100万個)
# 10万個
100000 entries in table, 65536 buckets
number of buckets with 0 entries: 5667
number of buckets with 1 entries: 33408
number of buckets with 2 entries: 17592
number of buckets with 3 entries: 5513
number of buckets with 4 entries: 2389
number of buckets with 5 entries: 599
number of buckets with 6 entries: 284
number of buckets with 7 entries: 61
number of buckets with 8 entries: 20
number of buckets with 9 entries: 3
number of buckets with 10 or more entries: 0
average search distance for entry: 1.6
# 100万個
% array statistics arr
1000000 entries in table, 1048576 buckets
number of buckets with 0 entries: 502271
number of buckets with 1 entries: 276353
number of buckets with 2 entries: 168961
number of buckets with 3 entries: 51585
number of buckets with 4 entries: 31912
number of buckets with 5 entries: 7806
number of buckets with 6 entries: 6553
number of buckets with 7 entries: 1340
number of buckets with 8 entries: 1086
number of buckets with 9 entries: 344
number of buckets with 10 or more entries: 365
average search distance for entry: 1.8要素名に数字を使用した場合、10万個程度なら10個以上のエントリ数があるバケットはないですが、100万個になると、10個以上のエントリ数があるバケットが365個も出来ました。
上のサンプルは、要素名に数字を使用した場合なので文字列を使用した場合は、ハッシュ値が違ってくるので、統計情報の出力結果も上記とは違う可能性があります。
ちなみに、このコマンドの存在意義って何?
個人的な見解を述べると、Tclまたはライブラリの開発者や、データベース関連でシビアなチューニングが必要な場合など、限られた用途でしか使わないのではないかと思う。
他にこんな使い方があるよ。と言うのがあれば教えて頂きたいですね。